Transfert d'un qubit vibrationnel dans un réseau moléculaire confiné (Stage de master 2)

Ce stage s'est déroulé au sein de l'équipe PhAs de l'Institut UTINAM UMR 6213 de l'Université de Franche-Comté sous la direction de Vincent Pouthier.

Contexte

L'avènement de la mécanique quantique a révélé des propriétés inédites des objets à l'échelle nanométrique. Parmi celle-ci, le concept d'états superposés occupe une place importante. Dans les années 80, des chercheurs comme R. Feynman [1] et D. Deutsch [2] ont montré que ce concept pourrait jouer un role clé dans la technologie du futur, notamment dans le domaine de l'informatique quantique. En informatique quantique le support de l'information est un qubit qui est un état superposé d'un système à deux niveaux.

Au cours de ce stage je me suis intéressé au transfert d'un tel qubit sous forme d'une superposition de deux états vibrationnels d'une molécule. Le transfert a lieu au sein d'une chaine moléculaire où sur chaque site un système à deux niveaux est présent. La création d'un état vibrationnel superposé sur le site N=1 entraine sa propagation dans la chaine via couplage dipolaire entre les molécules de chaque site. Je me suis donc intéressé au transfert d'un tel qubit du site N=1 à un site N=X et notamment à la qualité d'un tel transfert ainsi qu'aux problèmes qui lui sont associés, en particulier celui de la décohérence.

Le système

Le modèle théorique est le suivant :

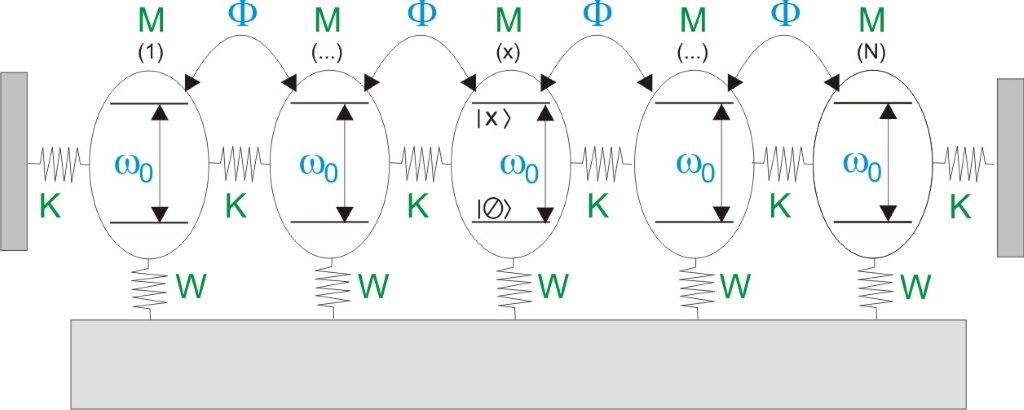
N systèmes à deux niveaux couplés entre eux, mais également couplés aux vibrations de phonon, c'est ce couplage qui va entrainer le phénomène de décohérence.

Le qubit est désigné sous le terme d'exciton, un hamiltonien H_S (S pour système) encode sa dynamique. L'Hamiltonien H_E (E pour environnement) encode les phonons (vibrations réseaux). Enfin un Hamiltonien ΔH encode le couplage entre l'exciton et les phonons.

L'Hamiltonien total prend donc la forme :

pour sa résolution, nous avons traité ΔH en perturbation sur H₀=H_S+H_E. Je ne reviens pas sur cette page sur les méthodes de calcul (voir ici).

Quelques résultats numériques...

Pour étudier la fidélité du transfert de l'exciton, la notion de propagateur en mécanique quantique est importante. Le propagateur est un opérateur qui "propage" l'état quantique à partir d'un état initial. Ici le module du propagateur |G_X1(t)| nous donnera la fidélité du transfert sur le site X sachant que l'exciton est parti du site 1. Si |G_X1(t)| = 1 le transfert sur le site X est parfait. En l'absence de couplage avec les phonons et pour un réseau infini, la solution du propagateur est bien connue, il s'agit de la fonction de Bessel de première espèce J_X(2Φt). Compte tenu du comportement des fonctions de Bessel on comprend bien que plus X est grand plus le module sera petit, c'est ce qu'on appelle le caractère dispersif du réseau. Il est donc impossible de réaliser un transfert avec une grande fidélité avec un réseau de taille infinie.

Si nous nous plaçons dans un réseau fini en revanche, la cohérence du qubit peut réapparaitre sur le site souhaité à un instant donné, ce phénomène porte le nom de récurrences quantiques ou "revivals" [3]. L'animation qui suit montre la dynamique du qubit dans le temps et sur chaque site. P est le module du propagateur qui vaut bien 1 à t=0 sur le site de depart (X=1).

On voit nettement réapparaitre des pics sur certains sites dans le temps. Ces pics qui ne sont pas des "revivals" complet car le système est grand N=30 sites, il n'est cependant pas à exclure qu'une copie parfaite de l'état de départ (par exemple sur le site X=30 de réception) arrive plus tard dans le temps.

La figure qui suit montre le module du propagateur |G_N1(t)| sur le site N dernier site du réseau ou site de réception.

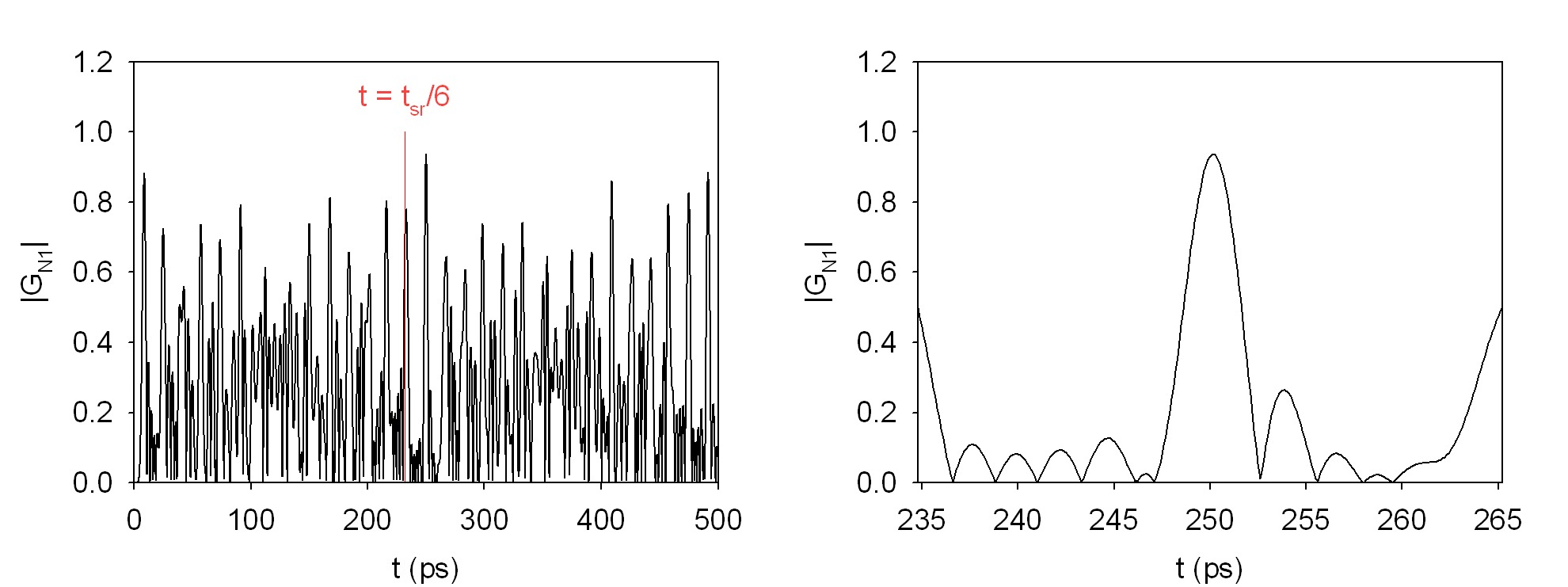
ici plusieurs "revivals" sur le site N sont bien visibles. A droite la figure montre un zoom sur le "meilleur" revival obtenu dans le temps de simulation.

Introduisons maintenant le couplage avec les vibrations du réseaux ou phonons. Un nouveau phénomène va faire son entrée, celui de la décohérence bien visible sur la figure qui suit.

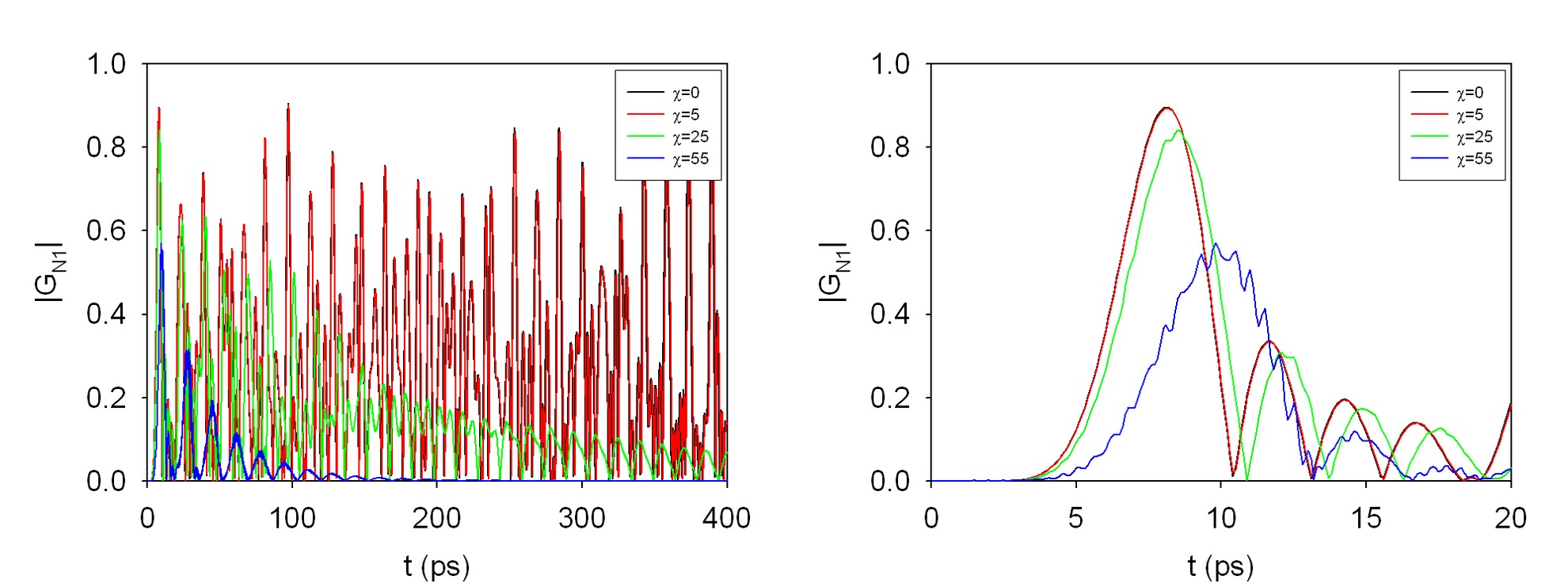
Ici nous voyons l'évolution dans le temps de |G_N1(t)| en fonction du couplage aux phonons. En noir sans couplage, en rouge avec un couplage un peu plus important, en vert un couplage plus fort encore enfin en bleu un couplage encore plus fort. On voit nettement que le phénomène de décohérence vient "détruire" la cohérence de l'état et même les revivals sont inexploitables assez rapidement. A droite, il s'agit d'un zoom sur le premier pic correspondant au premier passage du qubit sur le site N.

Nous comprenons donc bien que pour le transfert d'un qubit de façon efficace un réseau infini n'est pas envisageable à cause du phénomène de dispersion. En revanche un système confiné permet le transfert grâce aux phénomènes de récurrences quantique. Malheureusement comme toujours dans ce type de problème le phénomène de décohérence détruit la possibilité d'un transfert efficace. Pour plus d'informations sur le transfert de ce type de qubit en présence de phonon je vous invite à lire mon mémoire de Master 2 présent dans la section suivante.

Mémoire de M2

Références