Chaos dynamique dans le problème à trois corps restreint (Thèse de Doctorat)

Dynamique fractale

Dans cette partie, comme dans les deux autres, nous nous intéressons au problème à trois corps restreint. Ici nous limitons la dynamique au plan du système binaire, cela nous place dans le système dit "problème à trois corps restreint plan".

Au contraire des études précédentes, nous avons intégré numériquement les équations du mouvement. Comme les trajectoires sont susceptibles de passer très proche des masses composant le binaire nous avons régularisé les potentiels à l'aide d'une méthode Levi-Civita.

Le but de cette analyse est de nous concentrer sur les orbites éjectées du système. Par analogie à la mécanique quantique nous parlerons d'orbites ionisées. Pour ce faire un "rayon de ionisation" sera supposé autour du binaire. Au delà de ce rayon les particules sont considérées comme perdues. Ces différents aspects sont résumés sur la figure qui suit :

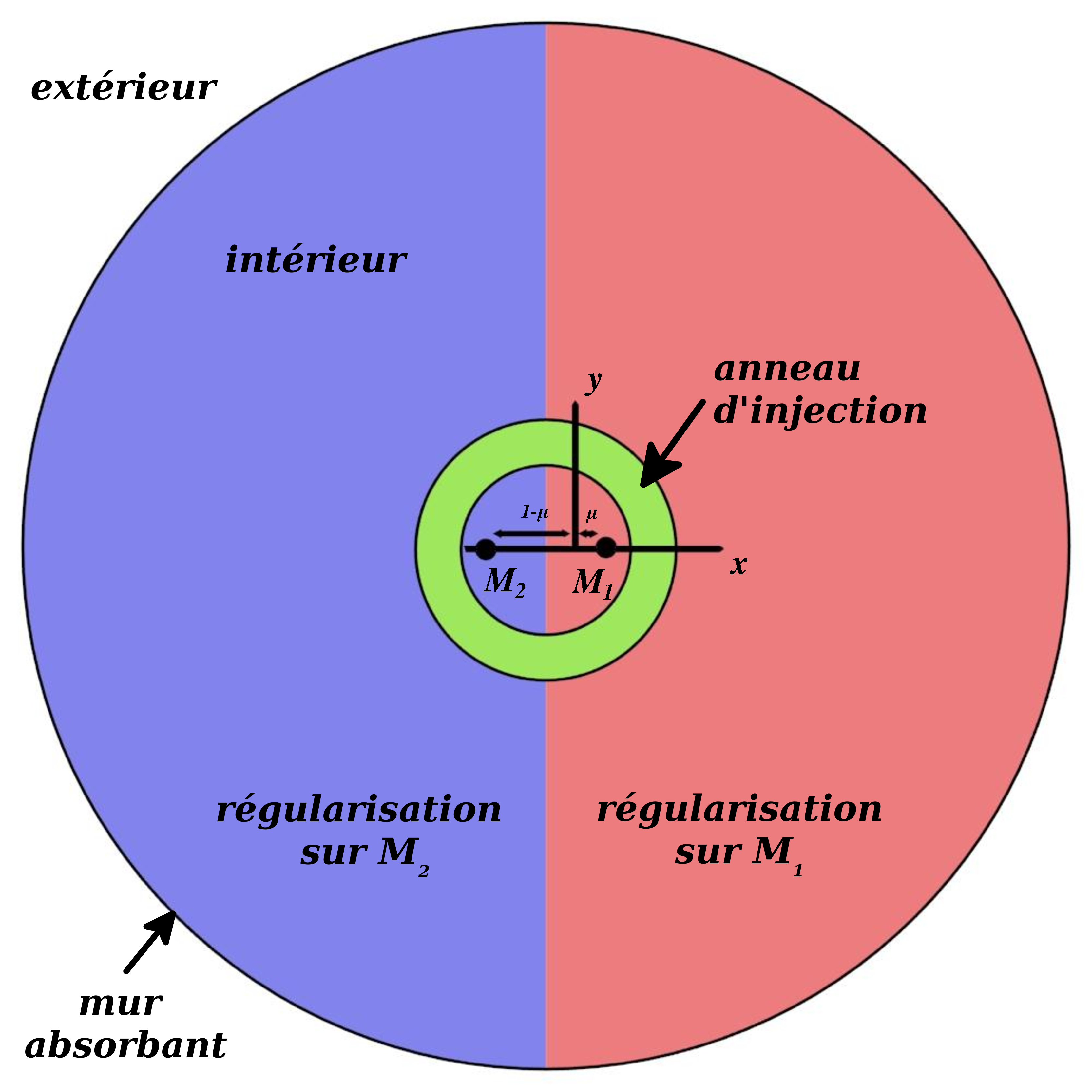
Dans ce cas nous nous trouvons dans le repère synodique (repère dans lequel le binaire est fixe). L'anneau vert représente l'anneau dans lequel nous "posons" les particules à t=0. La zone bleue correspond à une régularisation sur la masse M₂ la zone rouge sur la masse M₁. Le mur absorbant représente le rayon à partir duquel les particules sont considérées ionisées.

Ici nous nous intéressons au répulseur étrange qui est l'analogue des attracteurs étranges. Sans entrer dans les détails de ces concepts, nous appelons attracteur les zones de l'espace des phases qui semblent attirer les orbites. A contrario, les répulseurs sont les zones qui semblent "évacuer" les orbites. Nous avons affaire à un répulseur car les orbites que nous allons observer sont des orbites "sortantes".

Les attracteurs/répulseurs ont la particularité, dans le cas des systèmes chaotiques, d'avoir une géométrie fractale. La géométrie fractale a été développée par Benoît Mandelbrot [1]. Il s'agit d'objet dont la dimension n'est pas entière. Bien que cette définition soit insuffisante, nous la conserverons ici pour plus de simplicité. Pour plus d'informations, j'invite le lecteur à lire le dernier chapitre de ma thèse. L'un des attracteurs les plus connus est le célèbre attracteur de Lorenz [2], dans la culture populaire, il est le symbole du concept de chaos et de l'effet papillon.

Quelques résultats numériques...

En effectuant une section de Poincaré dans l'espace des phases selon la coupe (x,y) (espace réel), nous obtenons, pour les trajectoires non encore éjectées après 10 rotations du binaire, les sections de Poincaré suivantes :

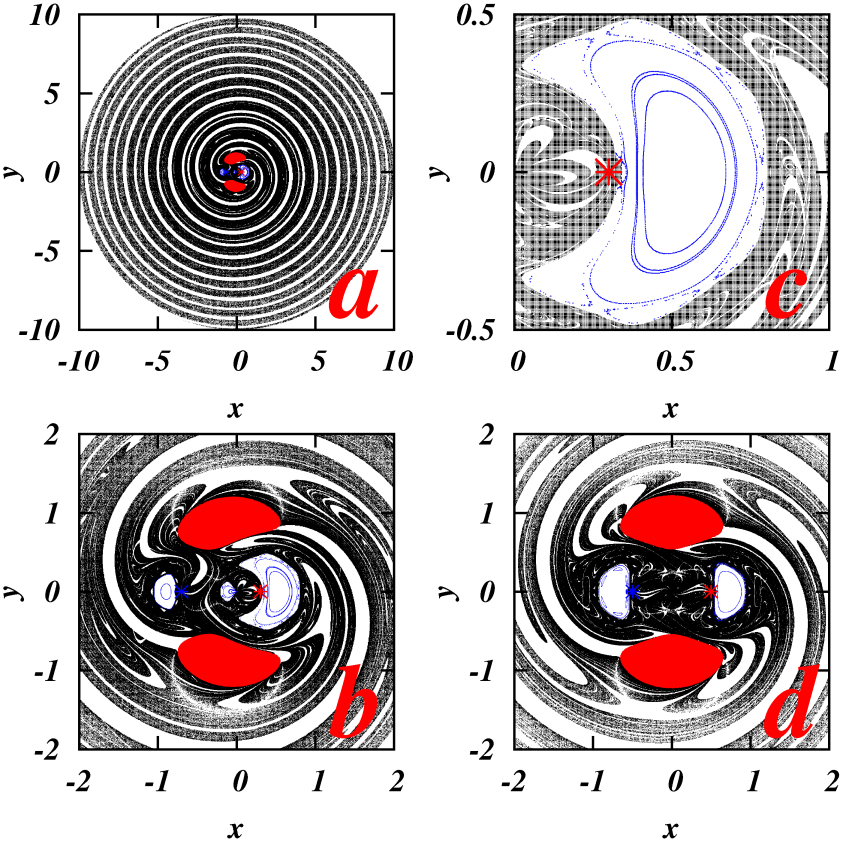
a),b) et c) : Section de Poincaré dans le plan (x,y), en noir les trajectoires qui vont être éjectées du système. En rouge : les zones interdites dans lesquelles le module de la vitesse au carré est négatif. Les lignes bleues sont les orbites stables de la dynamique à l'intérieur des îlots de KAM. Ces trois sections sont réalisées avec un paramètre de masse μ=0.3 (masse 1 : M₁=0.7, masse 2 : M₂=μ=0.3) et sur une surface d'énergie E=-1.5. Le panneau d) a un paramètre de masse μ=0.5 (deux masses identiques) et est généré sur une surface d'énergie E=-1.5.

Comme on peut le voir sur la figure précédente, la structure spiralée et fractale du répulseur étrange est bien visible. Par une technique de Box-Counting nous mesurons la dimension fractale de l'objet à D₀∼1.74 [3].

De nombreux autres résultats ont été obtenus concernant notamment les temps de survie des particules dans le système binaire. Ces résultats sont mis en relation avec la présence ou non d'îlots de KAM qui ralentissent la dynamique et qui ont un effet de "colle" sur les particules retardant ainsi leurs éjections. Pour plus d'informations concernant ces travaux j'invite à lire nos articles dans la section publication.

Retour vers : Chaos dynamique dans le problème à trois corps restreint

Références