Chaos dynamique dans le problème à trois corps restreint (Thèse de Doctorat)

Les comètes

Les comètes sont de petits objets en orbite autour du Soleil qui ont la particularité d'avoir une orbite dont l'excentricité et le demi-grand axe sont importants. Pour ces orbites dites "quasi-paraboliques" c'est le potentiel gravitationnel du Soleil qui domine.

Cependant, à l'approche de leurs périhélies, ces comètes "ressentent" les potentiels gravitationnels des planètes. Sur la figure qui suit nous pouvons voir une modélisation en 3D de l'orbite de la comète de Halley pour 3 passages.

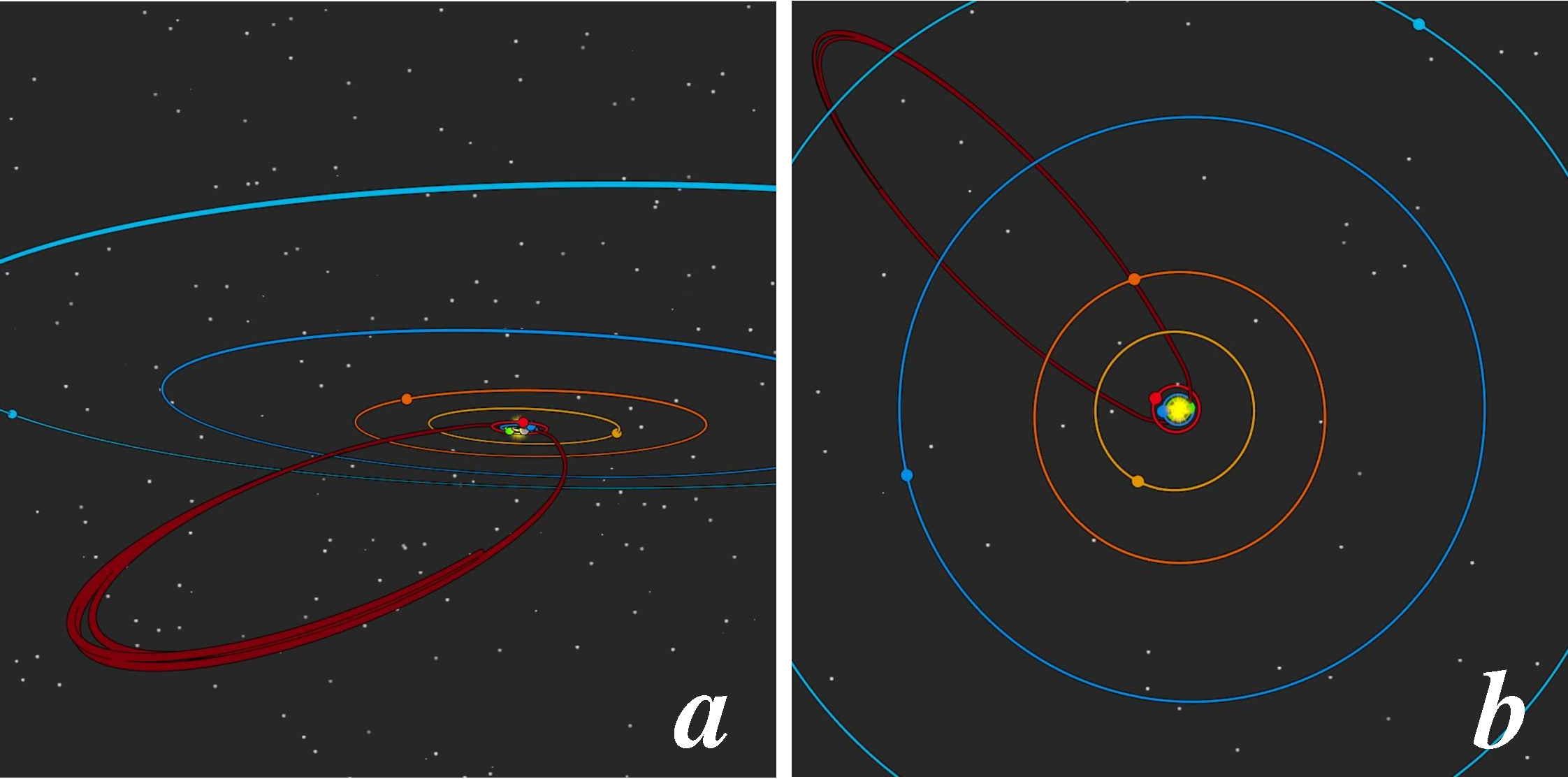
a) En rouge, une vue arbitraire où nous voyons l'aphélie. Les variations de l'orbite pour les trois passages sont caractéristiques des variations d'énergies dont nous allons parler ensuite. b) En projection "orthographique". Les différents cercles de couleurs représentent les orbites des planètes.

En première approximation, on peut donc affirmer que le mouvement des comètes se décompose en deux dynamiques différentes : une dynamique loin des planètes où le système se ramène à un problème à 2 corps et une dynamique à plusieurs corps à proximité du périhélie. Parmi les planètes, la contribution majeure est celle de Jupiter dont la masse est 1000 fois plus petite que celle du Soleil. Sur la base de cette première approximation, nous pouvons donc négliger la perturbation des autres planètes. Cela offre une piste de résolution approchée du problème à 3 corps restreint dans le cas bien particulier des orbites quasi-paraboliques.

Ces systèmes ont une dynamique frappée qui suit le schéma : énergie constante ==> saut brutal en énergie ==> énergie constante. Lorsqu'elle est à son aphélie, la comète ressent uniquement le potentiel du Soleil, la dynamique est à 2 corps et donc à énergie constante. Le passage à trois corps (Soleil, Jupiter, comète) vient perturber l'énergie qui va changer sur un court laps de temps. Après cela, le système retrouve une énergie constante. La figure qui suit, issue d'une simulation numérique, évoque ce comportement.

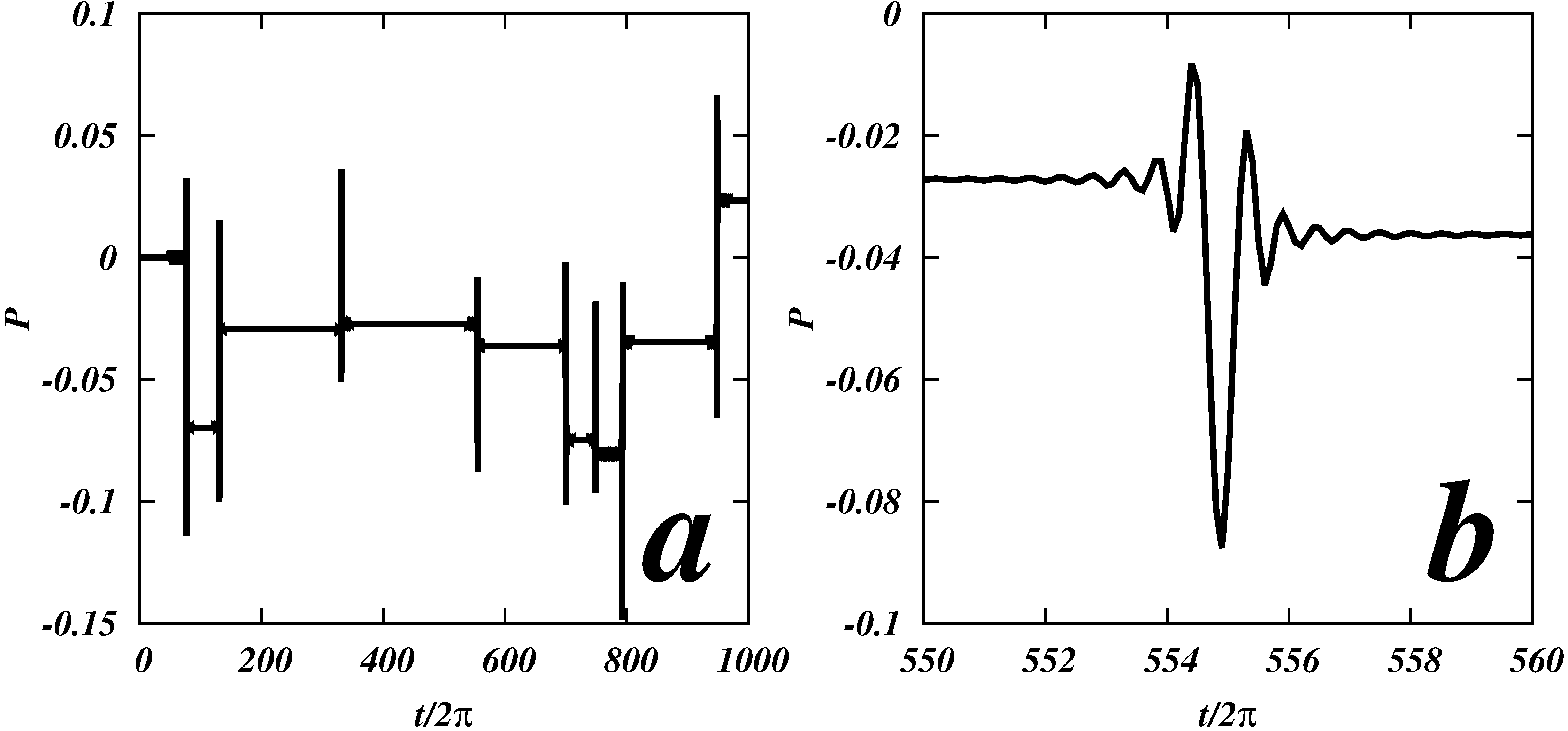
où P est l'énergie du système. On peut voir sur a) que l'énergie évolue par sauts successifs, c'est une dynamique kickée. b) Un zoom sur l'un des sauts qui révèle des oscillations que l'on peut expliquer par la théorie des perturbations que nous n'évoquerons pas ici.

Application symplectique

Il a été montré que par une théorie des perturbations, une application symplectique pouvait émerger et être utilisée pour ce type de dynamique [1] [2]. Cette application s'écrit :

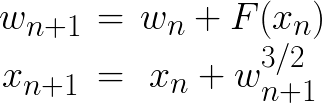
où

• w est l'énergie de la particule et donc l'inverse du demi-grand axe de son orbite.
• x est la phase du corps secondaire, il s’agit de l'angle polaire du second corps dans sa rotation circulaire autour du premier.
• n est le nombre de passage au périhélie de la particule.
• F(x_n) est la fonction perturbatrice due à la présence du corps secondaire. Elle retire ou donne de l'énergie (on l'appelle fonction kick).
• Enfin w_n+1^-3/2 est simplement la troisième loi de Kepler.

Quelques résultats numériques...

Au cours de notre étude du problème [3], nous avons calculé cette fonction perturbatrice par ce qui se ramène au calcul du travail sur une orbite particulière. Concrètement, nous plaçons numériquement la comète sur une orbite parabolique et nous faisons évoluer la dynamique en obligeant celle-ci à rester sur cette orbite. Le calcul du travail sur cette orbite nous donne l'énergie gagnée ou perdue par la comète en fonction de la phase du binaire Soleil-Jupiter (angle résultant de la rotation du binaire) au moment du passage au périhélie.

Nous pouvons montrer que le saut en énergie généré par la présence de chacune des planètes du Système Solaire est la somme des fonctions kick des systèmes Soleil-planète pour une phase donnée. Il est tout à fait possible d'utiliser le même procédé que précédemment pour calculer la fonction kick associée à n'importe quelle planète du Système Solaire. Après ce travail nous avons obtenu les résultats pour les fonctions kick suivants :

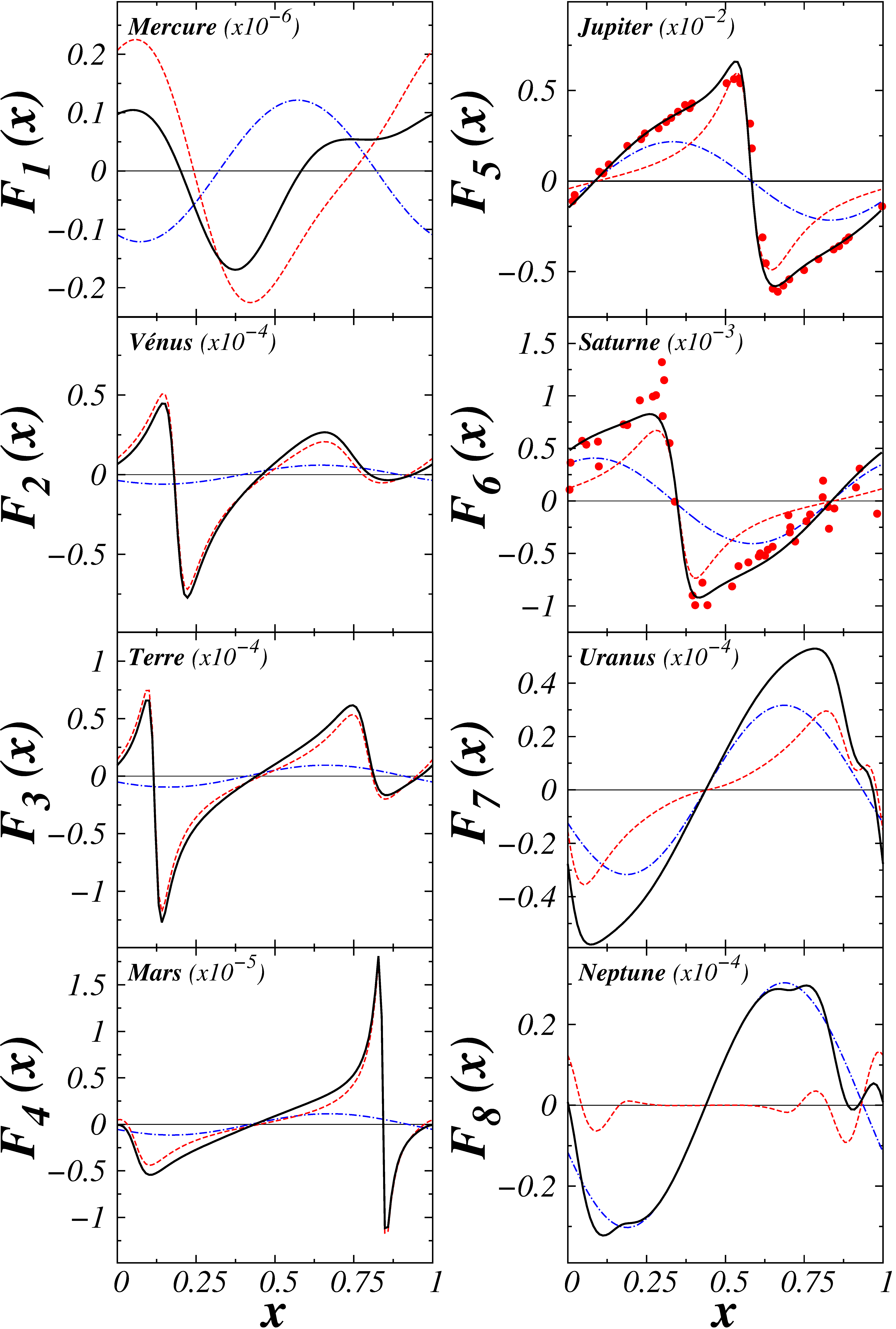
où nous avons les formes des fonctions kick pour toutes les planètes du Système Solaire. Je ne commente pas les différentes informations que nous révèlent ces tracés. Il faut surtout se concentrer ici sur les courbes noires qui nous donnent la valeur du saut en énergie ressenti par la comète au moment de son passage au périhélie en fonction de la phase x du binaire considéré.

Le type d'application symplectique vu plus haut, peut être représenté par une section de Poincaré dans l'espace des phases. Afin de ne pas surcharger cette page d'informations, nous pouvons dire que cette section de Poincaré est très proche de celle de la partie suivante concernant la capture de la matière noire ici. Pour plus d'informations concernant ces travaux, j'invite à lire nos articles dans la section publication.

Retour vers : Chaos dynamique dans le problème à trois corps restreint

Références