Chaos dynamique dans le problème à trois corps restreint (Thèse de Doctorat)

La matière noire

Le concept de matière noire est né dans les années 30. Il a été introduit par l'astrophysicien Fritz Zwicky [1]. Zwicky l'utilisa pour comprendre la masse à priori manquante de l'amas de galaxies de Coma pour permettre sa structure actuelle. Dans les années 60-70 les premières courbes de vitesse de rotations des galaxies montrèrent que la vitesse de rotation des étoiles autour du centre ne décroît pas selon une loi Keplerienne. Encore une fois une masse invisible ou matière sombre doit être ajoutée pour comprendre ce comportement. Au début des années 70 l'ajout d'un halo sphérique massif dans les simulations numériques de galaxies permet de les stabiliser (Jeremiah Ostriker [2]).

Qu'est ce que la matière noire ? En réalité personne ne le sait... Il s'agit dans tout les cas d'une matière massive n'intéragissant pas avec le champ électromagnérique. Deux pistes sont alors possibles :

• Les MACHOs (Massive Compact Halo Objects) : De gros objets massifs.
• Les WIMPs (Weakly Interacting Massives Particles) : Des particules n'interagissant pas avec le champ électromagnétique mais uniquement avec le champ gravitationnel (DMP pour Dark Matter Particle).

Il est important de noter qu'une théorie concurrente à la matière noire appelée théorie MOND pour Modified Newtonian Dynamics ne fait pas appel à la matière noire mais à une modification des lois de la gravitation.

De la dynamique d'une comète à la dynamique des DMP

Nous nous plaçons dans le contexte du halo de matière noire englobant la Galaxie. Les particules de matière noire passent donc à proximité des systèmes composant la Galaxie. Dans le cas où elles rencontrent un système simple : étoile, trou noir... les particules sont simplement diffusées gravitationnellement sur le système, en revanche si le système est double une interaction à trois corps peut précipiter leurs captures. L'idée est donc d'étudier comment ces phénomènes de captures peuvent modifier localement la densité moyenne du halo.

Avec un unique corps en x=0, y=0 il y a seulement diffusion :

Avec deux corps en rotation dont le centre de masse se situe en x=0, y=0 il peut y avoir capture :

Pour simuler la dynamique de ces particules à proximité de systèmes binaires, il est possible d'intégrer les équations du mouvement mais une autre technique, issue de l'étude de la dynamique des comètes autour du soleil [3], [4] perturbé par la présence des planètes, est utilisable [plus d'infos ici]. Cette technique repose sur la transformation de l'hamiltonien de la dynamique en une simple application symplectique. Cette transformation n'est possible que suite à une théorie des perturbations. Il faut, en conséquence que la masse du corps secondaire soit faible devant la masse du corps principal, typiquement M_secondaire/M_principal = 1/1000. Cette condition est remplie dans le cas de Jupiter et du Soleil dans le système Solaire.

Une fois cette condition réalisée, l'application symplectique décrivant la dynamique d'une particule de masse négligeable devant le binaire (problème à trois corps restreint) est la suivante :

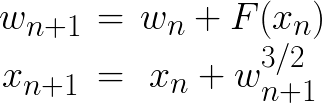
où

• w est l'énergie de la particule et donc l'inverse du demi-grand axe de son orbite.
• x est la phase du corps secondaire, il s’agit de l'angle polaire du second corps dans sa rotation circulaire autour du premier.
• n est le nombre de passage au périhélie de la particule (on peut montrer que la perturbation peut se concentrer au périhélie voir [4]).
• F(x_n) est la fonction perturbatrice due à la présence du corps secondaire. Elle retire ou donne de l'énergie (on l'appelle fonction kick).
• Enfin w_n+1^-3/2 est simplement la troisième loi de Kepler.

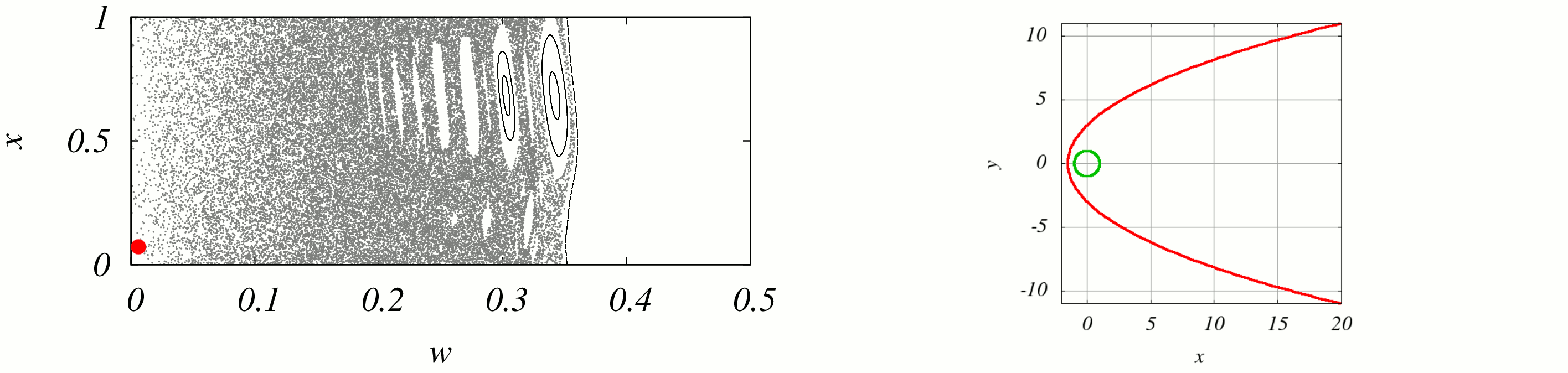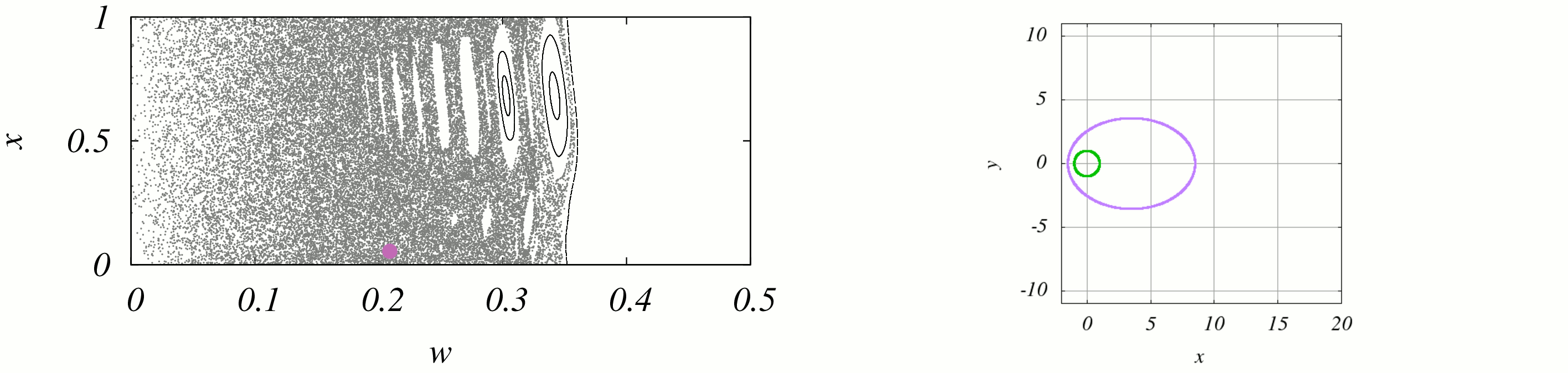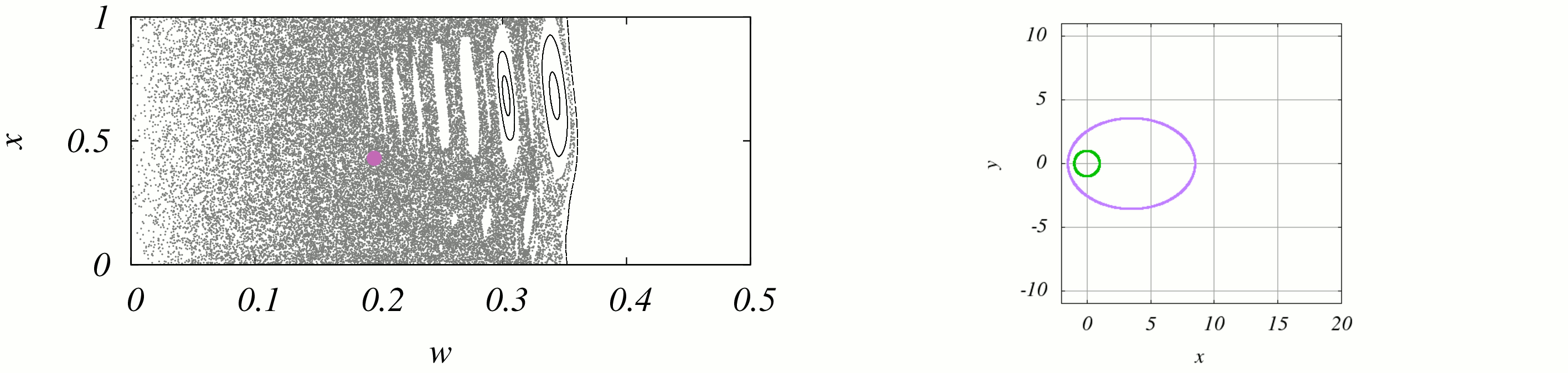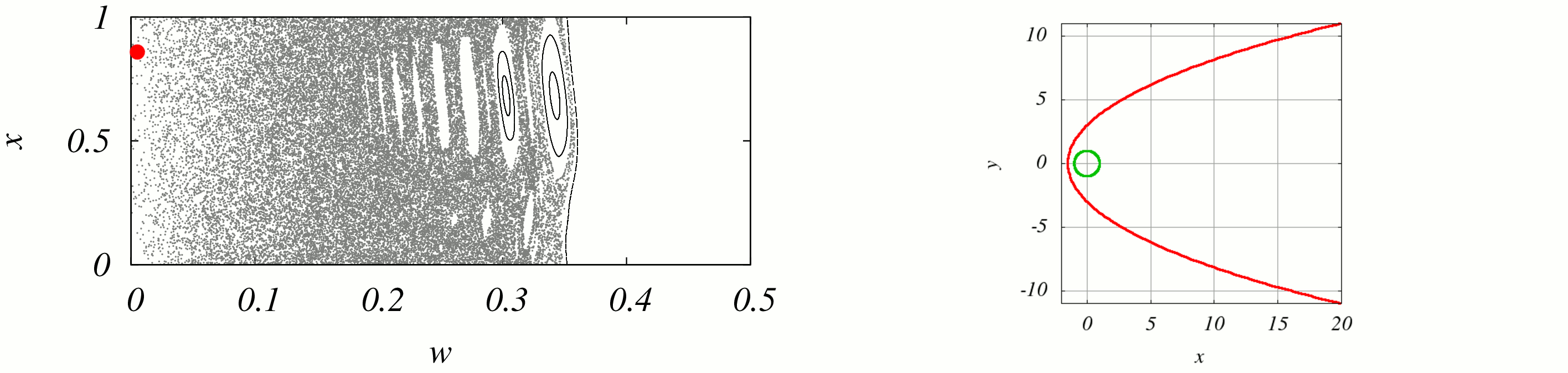
Sur cette animation on voit à gauche la position dans la section de la particule, à droite l'orbite dans l'espace réel que cela implique. On voit bien sur la figure de gauche le caractère chaotique de la dynamique : pour les énergies faibles le chaos domine.

Enfin en temps d'itérations réel la diffusion de la particule dans sa section donne :

On voit nettement dans le bas de la section où le chaos est généralisé que la particule diffuse librement (mouvement stochastique) en revanche pour des énergies plus grandes sa diffusion est bloquée ou ralentie par la présence d'îlots (zone blanche) appelé tores invariants de KAM (ce sont les reliquats de la dynamique non perturbée). La diffusion se poursuit jusqu'à une limite appelée courbe invariante de KAM qui limite de manière hermétique la diffusion (au delà la dynamique n'est plus chaotique mais à nouveau régulière).

Quelques résultats numériques...

Imaginons à présent simuler la dynamique d'un très grand nombre de particules en utilisant l'application symplectique... L'utilisation de l'application est intéressante car elle permet une multitude d'interprétations issues de la théorie du chaos, qui plus est, il s'agit de simples itérations, la simulation numérique est par conséquent moins gourmande en ressource numérique et en temps de calcul qu'une intégration des équations du mouvement.

Je vais présenter ici un unique résultat numérique (pour plus d'infos voir [5]) qui est l'évolution de la capture avec la vitesse du second corps. La courbe qui suit représente le facteur d'accroissement de densité de matière noire autour du binaire grâce à la capture, par rapport à la densité de matière noire moyenne de la Galaxie, le tout en fonction de la vitesse de rotation du binaire.

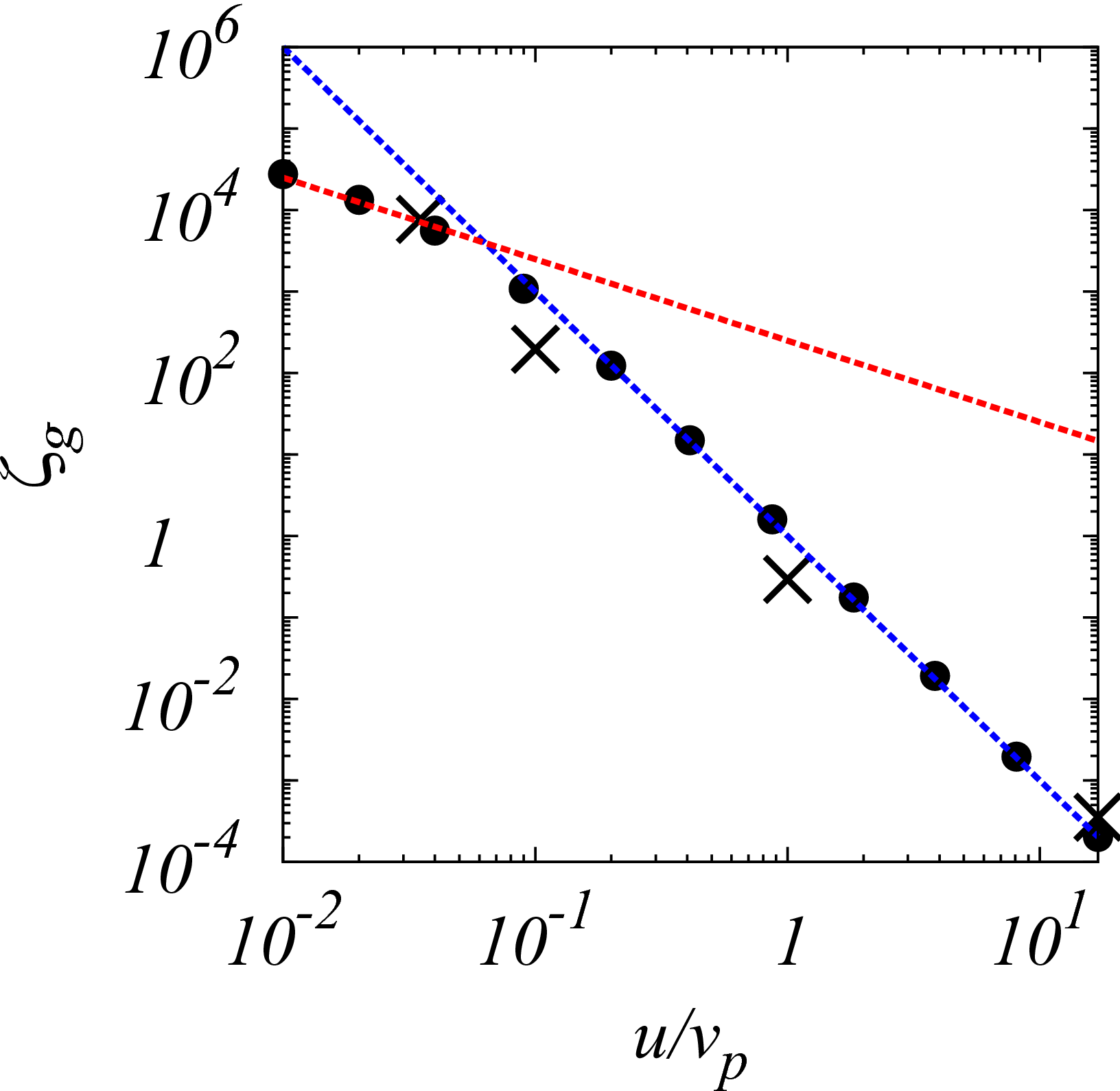
Ici plus u/v_p diminue, plus la vitesse du binaire augmente. Nous voyons donc bien que la densité subit une augmentation importante elle est notamment environ 10 000 fois plus grande autour de binaires très rapides (pour u~0.035 soit une vitesse de 2% de la vitesse de la lumière).

L'utilisation de l'application symplectique permet donc de mettre en évidence un accroissement de masse de matière noire non négligeable autour des systèmes doubles rapides. Un problème restant tout de même de taille est la limite de cette technique à un ratio de masse de 1/1000 du binaire (par exemple : système étoile-trou noir). Pour augmenter ce ratio on est obligé d'intégrer les équations du mouvement, il s'agit de l'un des projets en cours de réalisation... Pour plus d'information concernant ces travaux j'invite à lire nos articles dans la section publication.

Voici une vidéo réalisée alors que je préparais ma thèse. Elle résume l'ensemble de cette étude.

Retour vers : Chaos dynamique dans le problème à trois corps restreint

Références